Aperture-Fed Waveguide Horn Antenna

Horn dimensions calculator

Typical Characteristics
Bandwidth	Gain	Size	Impedance	Pattern	Polarization
40%	9dBi - 18dBi	$> \lambda$	Waveguide fed	Directional	Linear

The aperture-fed waveguide horn antenna is a common antenna that is widely used in systems which require a high efficiency directive antenna. This antenna is built nearly identically to the pin-fed waveguide horn antenna, except for the fact that it is not fed via a coaxial connector. This type of antenna is built by means of flaring the front of an open ended waveguide, this flare takes on the shaped of a horn. This horn shape directs radio waves into a high gain beam of energy. Horn antennas are widely used to as feeder antennas which often feed a parabolic dish increasing the gain of the total system.

A horn antenna is commonly used as a universal standard for calibration and gain measurements, these types of horns are often referred to as standard gain horns.

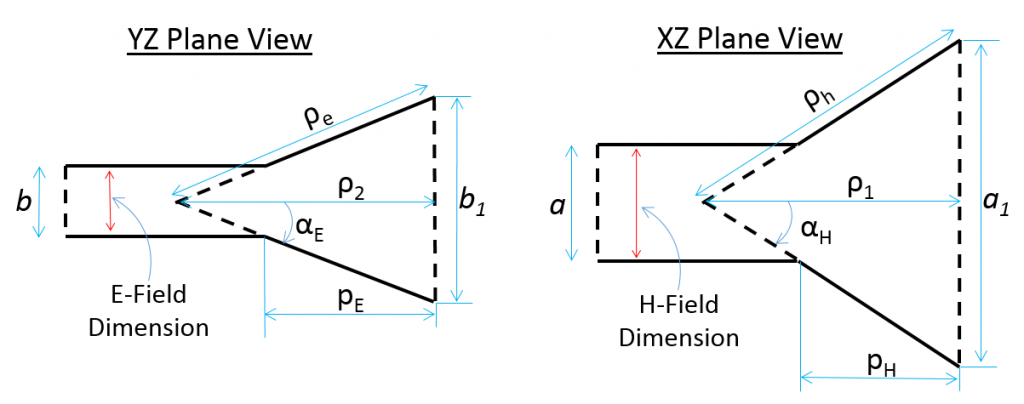
Equations for determining the parameters below are found at the end of this article.

Aperture Fed Pyramidal Horn Parameters

A well designed pyramidal horn antenna can have a peak gain between 9 and 18dBi, with some horns having as much as 25dBi of gain. The gain of horn antennas often increases as the frequency of operation is increased, this is due to the electrical length of the horn increasing as frequency is increased. Horns are considered to have a directional patterns.

Rotate Image by clicking on the image and moving the mouse

The radiation pattern of a horn antenna depends on the angle $\alpha_E$ and $\alpha_H$ as well as the final opening size $A$ & $B$ , this inherently affects $R_E$ & $R_H$ (note that $R_E = R_H$ ). If these parameters are properly optimized the performance of the horn can be optimized. Often these parameters are considered to be properly optimized if maximum gain is met in the shortest possible aperture length.

The bandwidth of a horn antenna is limited only by the frequency range of the waveguide selected. Each and every waveguide has a specific cutoff frequency. If the feed is not analyzed, the standard pyramidal horn works well over a sufficient bandwidth (typically greater than 40% bandwidth).

Typical waveguide match of a pyramidal horn

The cutoff frequency of the waveguide selected should be less than the operating frequency of the antenna. Once a waveguide is selected the equations below can be used to design the final pyramidal horn.

Equations and descriptions for determining the waveguide and pyramidal parameters:

See the Horn dimensions calculator to calculate these values.

RF waves can propagate in many different ways within a waveguide (often referred to as modes). For a pyramidal horn the dominant mode of the transverse electromagnetic wave is used in the rectangular waveguide. This is the $TE_{10}$ , this mode has the lowest attenuation of all modes in a rectangular waveguide, this mode has an electric field which is vertically polarized.

When building a waveguide make sure that the wave guide is the right size to work well (or at all) in the required frequency range:

$f_c=\frac{c}{2 a_{m}};\textrm{ } a_m=$ a in meters, ‘a’ from dimensions shown above

Maximum frequency which this waveguide should be used $f_{high}=1.89f_c$ .

Minimum frequency which this waveguide should be used $f_{high}=1.25f_c$ .

Height of waveguide $b=\frac{a}{2}$ .

These values can now be used to determine how much the horn should be flared. Most often it is optimal to optimize for a needed gain, in other words what is the smallest size the horn can be for a specific gain. To optimize the horn for size while achieving maximum gain the parameters $a_1$ $b_1$ , $\rho_e$ , $\rho_h$ , $p_E$ ,and $p_H$ must be found.

To fully optimize the above parameters $p_E$ must be equal to $p_H$ , using this equality the following formula can be used and solved for $\chi$ . All other parameters of this equation are known, where G is the linear gain of the horn.

$\left (\sqrt{2\chi} - \frac{b}{\lambda} \right )^2 (2 \chi - 1)= \left ( \frac{G_0}{2\pi} \sqrt{ \frac{3}{2\pi} } \frac{1}{ \sqrt{ \chi} } - \frac{a}{ \lambda } \right )^2 \left ( \frac{ G_0^2}{6 \pi^3} - \frac{1}{ \chi} - 1 \right )$ .

However, this equation must be solved iteratively; for a non-perfectly optimal solution, or for a starting point for the above equation the following formula can be used to solve for $\chi$ .

$\chi = \frac{G}{2 \pi \sqrt{2\pi} }$ .