Pin-Fed Pyramidal Horn

Horn dimensions calculator

Typical Characteristics
Bandwidth	Gain	Size	Impedance	Pattern	Polarization
>15%	9dBi - 18dBi	$> \lambda$	10 Ω to 250Ω	Directional	Linear

The pin-fed waveguide pyramidal horn antenna is a common antenna that is widely used in systems which require a high efficiency directive antenna. This type of antenna is built by means of flaring the front of an open ended waveguide, this flare takes on the shaped of a horn. The horn shape helps to transition the waveguide mode into a free-space mode, directing energy into a high gain beam. Horn antennas are widely used as feeder antennas. One main application for these types of feeder antennas is to feed a parabolic dish increasing the gain of the total system, of as a directive element for large phased arrays.

Pin-fed pyramidal horns are commonly used as a universal standard for calibration and gain measurements, these types of horns are often referred to as standard gain horns.

Equations for determining the parameters for building this type of antenna are found at the end of this article.

Pin-Fed Pyramidal Horn Parameters

A well designed pyramidal horn antenna can have a peak gain ranging between 9 and 18dBi, with some horns having as much as 25dBi of gain. The gain of horn antennas often increases as the frequency of operation is increased, this is due to the electrical length of the horn increasing as the frequency is increased. Horns are considered to have a directional patterns.

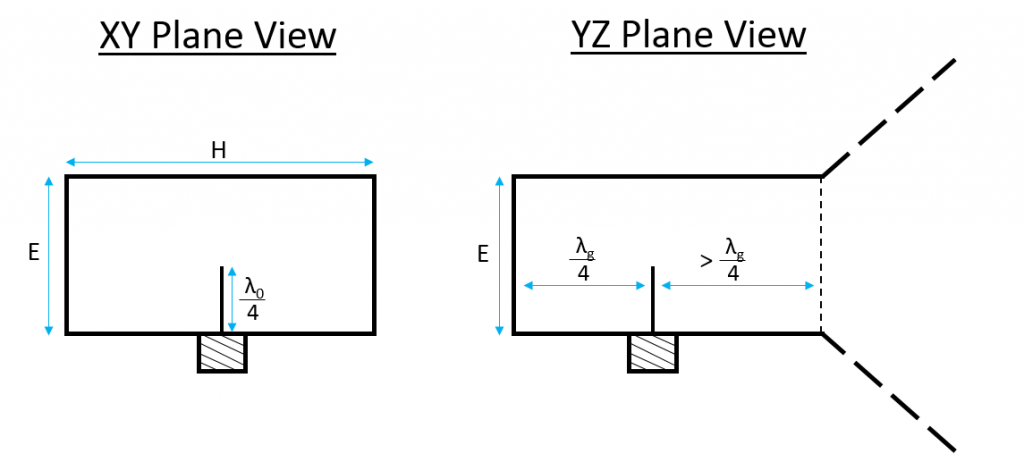
Horn antennas are often fed using a coax feed line with a $\lambda_0 / 4$ length “monopole” pin as shown in the figure below. The ground of the coax is electrically connected to the waveguide and the center connector is connected to the $\lambda_0 / 4$ pin which is inside the waveguide. The pin is generally offset from the back of the waveguide by $\lambda_g / 4$ where $\lambda_g$ is the guided wavelength, or the wavelength of the mode inside the waveguide.

Waveguide Pin Feed Dimensions

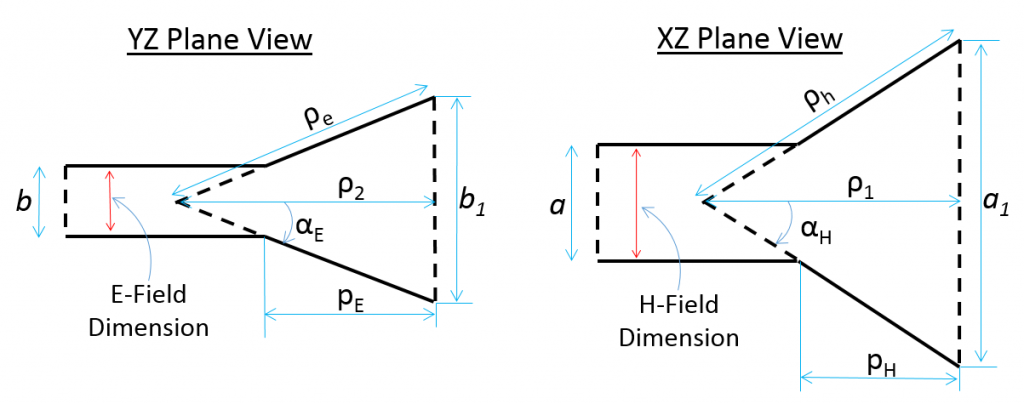
The radiation pattern of a horn antenna depends on the angle $\alpha_E$ and $\alpha_H$ (first figure) as well as the final opening size $A$ & $B$ , this inherently affects $R_E$ & $R_H$ (note that $R_E = R_H$ ). If these parameters are properly optimized the performance of the horn can be optimized. Often these parameters are considered to be properly optimized if maximum gain is met in the shortest possible aperture length.

Rotate Image by clicking on the image and moving the mouse

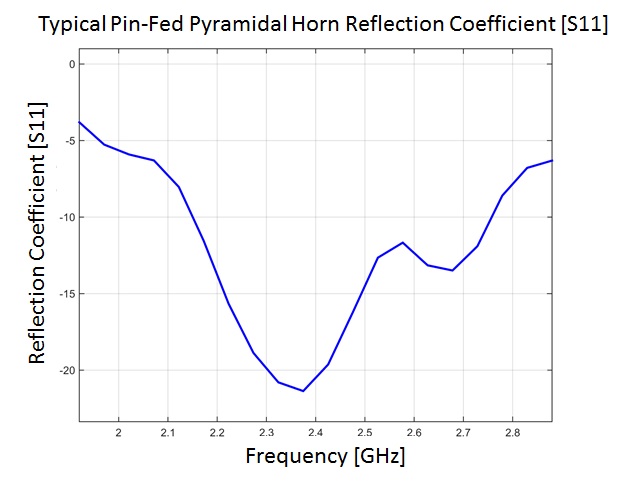
The bandwidth of a horn antenna is limited both by how the feed is designed and by the frequency range of the waveguide selected. Each and every waveguide has a specific cutoff frequency. If the feed is designed properly, the standard pin-fed pyramidal horn can works well over a sufficient bandwidth (typically greater than 15% bandwidth).

Typical Pin-Fed Waveguide Pyramidal Horn Match

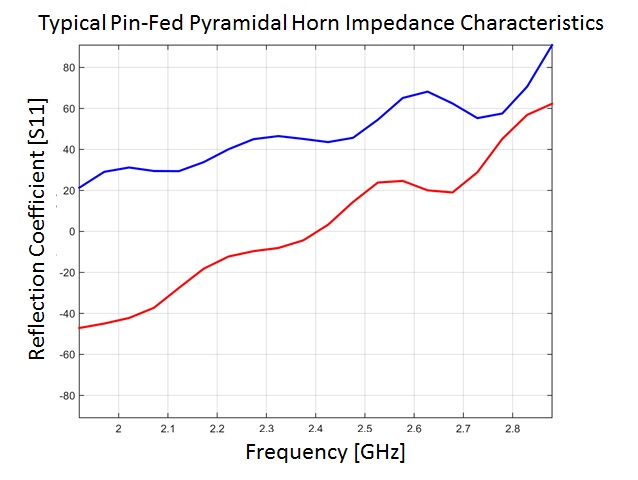
The natural input impedance of a waveguide is not easy to perfectly match to 50 Ohms across wide-band operation. The reason for the imperfect match is due to the $\lambda_g / 4$ waveguide spacing as well as the $\lambda_0 / 4$ pin length. The bandwidth and performance of the system can be increased by top loading the pin-fed, this capacitively loads the pin, allowing for a more shallow match which will effectively have a greater bandwidth potential. This along with optimizing the waveguide spacing can significantly increase the bandwidth of the pin-fed pyramidal horn antenna. The typical impedance characteristics of a standard pin-feed are shown bellow.

Typical Pin-Fed Pyramidal Horn Impedance Characteristics

The cutoff frequency of the waveguide selected should be less than the operating frequency of the antenna. Once a waveguide is selected the equations below can be used to design the final pin-fed pyramidal horn.

General Facts:

Larger Waveguide = Lower Frequency
Longer Flair = More Gain
Bandwidth Limited by Waveguide
Reflection Coefficient is Generally Low

Design Guidelines:

Waveguide dimensions
- $a=0.8382\lambda$
- $b=0.3925\lambda$
$\frac{R_{H0}}{R_H}=\frac{A}{A-a}$
$\frac{R_{E0}}{R_E}=\frac{B}{B-b}$
$G=\frac{4\pi}{\lambda^2}\epsilon_{ap} a_1 b_1$
To Increase Frequency:
- Decrease waveguide width & length
Increase Gain:
- Increase the size of aperture $a_1$ & $b_1$

Equations and descriptions for determining the waveguide and pyramidal parameters:

See the Horn dimensions calculator to calculate these values.

RF waves can propagate in many different ways within a waveguide (often referred to as modes). For a pyramidal horn the dominant mode of the transverse electromagnetic wave is used in the rectangular waveguide. This is the $TE_{10}$ , this mode has the lowest attenuation of all modes in a rectangular waveguide, this mode has an electric field which is vertically polarized.

When building a waveguide make sure that the wave guide is the right size to work well (or at all) in the required frequency range:

$f_c=\frac{c}{2 a_{m}};\textrm{ } a_m=$ a in meters, ‘a’ from dimensions shown above

Maximum frequency which this waveguide should be used $f_{high}=1.89f_c$ .

Minimum frequency which this waveguide should be used $f_{high}=1.25f_c$ .

Height of waveguide $b=\frac{a}{2}$ .

Now it is possible to determine the $\lambda_g / 4$ frequency:

$\lambda_{g}= \frac{ \lambda_0}{ \sqrt{1-\left( \frac{ \lambda_0}{ \lambda_{c}}\right )^2} }$ .

Now the size of the waveguide is known, the cutoff frequency, and the guided wavelength is known. These are all the parameters needed to make and feed the waveguide. Now it is possible to try and design a horn with optimal dimensions.

Now lets determine how much the horn should be flared. Most often it is optimal to optimize for a needed gain, in other words what is the smallest size the horn can be for a specific gain. To optimize the horn for size while achieving maximum gain the parameters $a_1$ $b_1$ , $\rho_e$ , $\rho_h$ , $p_E$ ,and $p_H$ must be found.

To fully optimize the above parameters $p_E$ must be equal to $p_H$ , using this equality the following formula can be used and solved for $\chi$ . All other parameters of this equation are known, where G is the linear gain of the horn.

$\left (\sqrt{2\chi} - \frac{b}{\lambda} \right )^2 (2 \chi - 1)= \left ( \frac{G_0}{2\pi} \sqrt{ \frac{3}{2\pi} } \frac{1}{ \sqrt{ \chi} } - \frac{a}{ \lambda } \right )^2 \left ( \frac{ G_0^2}{6 \pi^3} - \frac{1}{ \chi} - 1 \right )$ .

However, this equation must be solved iteratively; for a non-perfectly optimal solution, or for a starting point for the above equation the following formula can be used to solve for $\chi$ .

$\chi = \frac{G}{2 \pi \sqrt{2\pi} }$ .